2.1 THE SQUIRREL CAGE INDUCTION MOTOR
2.1.1 The
3-phase Motor
The normal induction motor operates only on a 3-phase
supply. It consists of a stator wound
with a 3-phase winding in slots on the inside of the yoke. The windings are distributed around the
stator so that in a so-called ‘2-pole’ motor their axes are spaced 120° apart.
Each winding end is brought out to a terminal. The other ends are usually star-connected
within the machine. In some instances
the machine may be delta-connected, in which case all six ends may be brought
out to six or three terminals.
If a 3-phase supply is connected to the three stator terminals, such an arrangement gives rise to a rotating magnetic field. This completes one revolution in one cycle of supply; that is to say, with a 60Hz system frequency the field rotates at 60 rev/s, and with a 50Hz supply at 50 rev/s. This is called the ‘synchronous speed’. (See ‘Fundamentals of Electricity 2’, Chapter 3.)
FIGURE
2.1
MAGNETIC FIELD, EMFs AND CURRENTS IN ROTOR
Inside the stator is a rotor which is free to rotate and
has no electrical connections to it - that is to say, no brushgear. The rotor could be of solid iron, but it is
more usually laminated and fitted with uninsulated copper or aluminium bars in
slots round its outer edge, the bars being short-circuited at both ends by
brazed metal rings, as shown in Figure 2.1.
The bars and rings together form a cage-like assembly,
and this form of motor, by far the most numerous, is called ‘squirrel
cage’. There are variations on this
arrangement, but they are not found offshore, and not often onshore.
Figure 2.1 shows only the rotor. The stator and its windings already described
in the earlier manual are not shown, but the rotating field which the stator
produces is indicated in blue. This is
the only manifestation of the stator that the rotor ‘sees’.
While the rotor is at rest and therefore stationary, the
rotating field from the stator passes through all the rotor conductors in turn,
generating emfs in them by Faraday’s Law of Induction. Because all the rotor bars are
short-circuited, these emfs cause currents to flow through the bars and
end-rings as indicated in red in the figure.
The direction of the currents will change as the passing field changes
from N to S and back again.
The rotor bar currents react with the magnetic field
surrounding them to produce a sideways mechanical force on each bar, as
explained in Chapter 6 of the manual ‘Fundamentals of Electricity 1’. By Fleming’s Left-hand Rule these forces act
on all bars in the same direction and produce a combined torque on the rotor in
the direction of the field rotation.
This causes the rotor to accelerate from rest. In more simple terms the rotor can be
considered as being ‘dragged around’ by the rotating field.
As the rotor accelerates, the relative speed of the
field passing it becomes less, the frequency and amount of the emfs and the
rotor currents get less, and the mechanical force on the conductors and the
torque on the rotor, after increasing for a time, also become less. Finally the rotor settles down to a speed
slightly less than that of the field (the synchronous speed), when the emfs are
at very low frequency and are just sufficient to maintain the rotor current and
torque against the load. This settled
speed is typically 1 to 2% below synchronous, and the difference is called the
‘slip’. For example, a 2-pole, 60Hz
motor would have a synchronous speed of 3 600 rev/mm; the motor nameplate may
show the motor’s rated speed as 3 540 rev/mm, which would indicate a slip of
1.67% at full-load. At less than
full-load the slip is reduced and the speed approaches nearer to
synchronous. Conversely, as mechanical
load is applied, the slip increases, and the rotor’s induced emf and hence its
current rises, which gives an increase in driving torque to meet the load.
Thus induction motors have nearly, but not quite, a
fixed speed just below synchronous, and it cannot be controlled (as in a d.c.
motor) except by complicated and expensive equipment which is not installed in
offshore or onshore installations. For
this reason it is often called an ‘asynchronous motor’.
As the rotor gathers speed, it generates increasing
back-emf in the stator, causing the stator current to fall. At full speed, as load is applied, the slip
and the rotor currents increase, causing increasing stator currents (and
therefore motor ‘load’) by transformer action.
When the creation of rotating fields was discussed in
the earlier manual it was explained that, with one stator winding per phase,
the field made one revolution per cycle.
If, however, there were two parallel windings per phase, making a total
of six windings disposed at 60° (instead of 120°) intervals, the field would make only half a revolution per
cycle. A machine so wound is called a
‘4-pole’ motor; at 60Hz its field rotation would be only at 1 800 rev/mm, and
this therefore would be its synchronous speed.
As already explained, the full-load speed is just below
synchronous, differing from it by the small slip, so that the nameplate rated
speed of 4-pole motors at 60Hz will be around 1 750 rev/mm. These in fact are far more numerous than the
faster 2-pole motors. Similarly
6-pole motors (synchronous speed at 60Hz 1 200 rev/mm) will have rated speeds of about 1 160 rev/mm. With 50Hz supply systems the rated speeds for 2-, 4- and 6-pole motors will be about 2 950, 1 475 and 980 rev/mm respectively.
6-pole motors (synchronous speed at 60Hz 1 200 rev/mm) will have rated speeds of about 1 160 rev/mm. With 50Hz supply systems the rated speeds for 2-, 4- and 6-pole motors will be about 2 950, 1 475 and 980 rev/mm respectively.
It should be particularly noted that the induction motor
is not strictly a constant-speed motor, as its speed varies over a small range
of up to about 2% between no-load and full-load. Neither is it a variable-speed motor in the
sense that it can be used for variable-speed drives, as can be done with d.c.
motors. For most practical purposes however,
such as for driving pumps, compressors and similar plant, it can be regarded as
a constant-speed machine. Only where exact
constant speed is needed would it be necessary to go to a synchronous motor.
2.1.2 The
Single Phase Motor
The 3-phase motor described above depends on the
creation of a rotating magnetic field from static windings in a 3-phase
stator. However, it is possible to
create a rotating field from a single-phase supply provided that it is split
into two parts whose space-displacement and time-displacement are equal - in
this case 90° instead of the 3-phase 120°. Such a motor is called a ‘split-phase’
motor. The principle is described in the
manual ‘Fundamentals of Electricity 2’, Chapter 3.
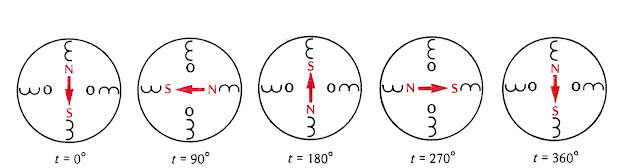
Figure 2.2 shows how the split is achieved. It has four pole windings spaced at equal 90° intervals round the stator.
Opposite pairs of poles have opposite polarities, so that, when one is
producing an N field, the other is producing an 5, and vice versa.
The other pair of windings, 90° displaced, are fed through a capacitor of sufficient size to cause
the current through the second pair of windings to lead by nearly 90° in time on that in the other pair.
Single-phase
Supply
FIGURE 2.2
SPLIT PHASE, SINGLE PHASE (CAPACITOR) INDUCTION MOTOR
FIGURE 2.3
SPLIT
PHASE MOTOR STATOR FIELD
Figure 2.3 shows the polarities at 90° (quarter-cycle) time intervals.
At time t = 360° (on the extreme right) the 12 o’clock
pole is N maximum and the 6 o’clock S maximum.
Both the 3 o’clock and 9 o’clock poles are zero because their currents,
leading 90° on those of the other two, are passing through zero at that
instant.
One-quarter of a cycle (90°) earlier, moving from right to left, at t = 270°, the 9 o’clock pole, whose current leads 90° on that of the 12 o‘clock, was at maximum N, and the 3 o’clock at
maximum S. The poles at 12 and 6 o’clock were zero because their currents were
passing through zero at that instant.
Similarly one-quarter of a cycle still earlier (t
= 180°) 6 o’clock was N and 12 o’clock was S, with 3 and 9 o’clock both
zero. And at t = 90°, 3 o’clock was N and 9 o’clock S, with
12 and 6 o’clock both zero. And so back
to t = 0°, which is the same as t = 360°.
It can be seen from Figure 2.3, moving now from left to
right - that is, from t = 0° to t =
360° - that the N-pole progresses steadily from 12 o’clock at t =
0°, through 3 o’clock, 6 o’clock and 9 o’clock back to 12
o’clock. The S-pole progresses in the
same direction but 180° behind.
Therefore a clockwise rotating field, completing one
revolution in one cycle of time, has been produced from a single-phase
supply. It should be added that the
above explanation has been idealised.
The current in the 3 and 9 o’clock poles will not lead the full 90° on that in the other poles because of resistance and inductance,
but the split is quite sufficient to produce an adequate rotating field. This arrangement is not so efficient as a
proper 3-phase motor, but it meets the requirements for smaller motors.
Once the rotating field has been obtained in this manner
from a single-phase supply, the squirrel-cage rotor will run up to speed and
follow it, with the usual slip, exactly as for a 3-phase motor.
When a split-phase single-phase motor has been run up to
speed, it will continue to run and to deliver power even if the capacitor
winding is disconnected. Therefore all
but the smallest of such motors have their 3 o’clock and 9 o’clock windings,
and the capacitor itself, short-rated.
Once the motor has run up, a centrifugal switch opens the capacitor
circuit. When the motor stops it
reconnects it. In such a motor the 3 and
9 o’clock windings are referred to as the ‘starting winding’ and the other as
the ‘running winding’. On very small
motors the centrifugal switch may be omitted and both windings left in circuit.
The split-phase motor is widely used for domestic
equipment, where only single-phase supplies are usually available. Like the 3-phase equivalent, it is
direct-on-line started and exhibits similar slip, torque and current characteristics. It is sometimes called a ‘capacitor motor’;
the capacitor is usually mounted on the outside of the motor case.
Other methods are sometimes used to achieve the phase
difference between the starting and running windings, but the capacitor method
is by far the most common.
2.2 THE WOUND MOTOR INDUCTION MOTOR
The induction motors so far described use a rotor of the
squirrel-cage type, in which the conductors are uninsulated and where the
rotor-bar currents, induced by the field passing at slip speed, are limited
only by the resistance of the bars themselves and of the end rings and by the
reactance of the rotor. There is no
external control of these currents. It will
be shown later that, when a motor is started by switching it direct onto line,
the initial starting currents are very high, and there is no means of
controlling them at the motor.
FIGURE 2.4
WOUND ROTOR INDUCTION MOTOR
Although these high starting currents are normally
allowed for in the design of the system, it is sometimes necessary to reduce
them. One way of achieving this is by
using a wound rotor. Such a machine has,
instead of a squirrel-cage rotor, one that is wound like a normal machine with
insulated conductors in slots. Three
separate phase windings are provided on the rotor, and they are brought out to
three sliprings, as shown in Figure 2.4.
Under normal running conditions the three sliprings are
short-circuited by an external switch or contactor, but during starting they
are connected to a set of variable resistances.
They introduce into the rotor circuit extra resistance which limits the
rotor current and hence the current drawn by the stator. These ‘starting resistances’ are progressively
reduced as the motor gathers speed (much like the old d.c. starters) until at
full speed they are shorted out altogether, and the machine behaves as a
squirrel-cage motor with short-circuited rotor bars.
It should be noted that the resistances are purely for
starting and are therefore only short-rated.
They are not for speed control, since speed is virtually constant and is
determined by the system frequency.
Inserting the rotor resistances has only a slight effect on the slip and
so very little effect on the speed.
Starting resistances for wound-rotor machines may be of
any variable-adjustment type, or they may be fixed with tappings selected in
turn by contactors where starting control is automatic. In some cases a liquid resistor is used where
three plates are gradually lowered into a tank containing an electrolyte; this
gives a continuously variable control.
Wound-rotor motors and their control gear are far more
expensive than the simple squirrel-cage motor.
None are installed in any offshore and few, if any, in onshore
installations.

+INDUCTION+MOTOR.jpg)

No comments:
Post a Comment