FAULTS
AND FAULT LEVELS
CONTENTS
FAULTS AND FAULT
LEVELS.......................................................................
SYMMETRICAL AND ASYMMETRICAL FAULTS.........................................
FAULT CALCULATIONS....................................................................................
IMPEDANCE.........................................................................................................
FAULT LEVEL.......................................................................................................
GENERATORS....................................................................................................
CABLES................................................................................................................
SOURCE IMPEDANCE......................................................................................
MOTORS...............................................................................................................
PRACTICAL EXAMPLES.....................................................................................
EARTH FAULTS..................................................................................................
FAULTS AND FAULT LEVELS
Before selecting a protection system we
must consider the kind of fault which may occur.
The principal types are:
·
3 Phase
(with or without earth)
·
Phase - to
- phase
·
Phase - to
-Earth
·
Double
Phase - to - Earth
Sometimes there are open-circuits
involved. Transformers and motors are
also subject to short circuits between turns of the same winding.
Only the 3 phase short circuit is a
balanced condition. The others are
unbalanced and require a knowledge of the method known as ‘symmetrical
components’ before they can be fully analysed.
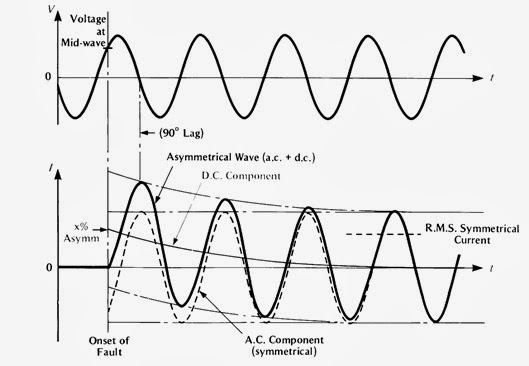
SYMMETRICAL AND ASYMMETRICAL FAULTS
When a short-circuit occurs, it may be between two of the three
lines of a 3-phase system, or it may involve all three. The fault current may
pass between phases as an arc which has some resistance and so limits the
current, or there may be metal-to-metal contact, a so- called 'bolted' fault,
where the impedance is zero. As an item of switchgear must be able to deal with
the most severe possible case it is always assumed that the fault is a 3-phase
bolted one, and that the whole circuit is mainly inductive with little
resistance.
FIGURE
4.1 -
PARTIAL CURRENT ASYMMETRY AT ONSET OF A FAULT
It is known that with an inductive fault the current which
immediately follows is in general partially asymmetrical. The asymmetry will be
complete (100%) if the fault occurs at the instant of a voltage zero. If it
occurs at a voltage peak, positive or negative, the asymmetry is zero (0%) -
that is to say, the current wave is then wholly symmetrical.
Figure 4.1 shows the general case where the asymmetry is partial
(between 0% and 100%). The point on the voltage wave at which a fault may occur
is of course entirely random. So therefore is the degree of asymmetry which
will occur in any particular case.
This asymmetrical current wave is regarded as resolved into two
parts: a symmetrical a.c. wave plus a steady but decaying 'd.c. component'
whose rate of decay is mainly the R/L ratio of the fault circuit; the d.c.
component is also shown in Figure 4.1. The quicker the decay of the d.c.
component, the quicker the fault current resumes symmetry.
With complete asymmetry the first peak of the asymmetrical current
wave is almost double the amplitude of the a.c. component at that time - that
is 2 x Ö2 (= 2.82) times its rms value. However
by the time the first current peak is reached there has already been some decay
of the d.c. component, and it is usual to take the first current peak as
approximately 2.55 times the rms value of the a.c. component. This figure
however may differ slightly in special cases.
FIGURE 4.2 -
THREE PHASE CURRENT ASYMMETRY (GENERAL CASE)
Although Figure 4.2. shows the a.c. component as having constant
amplitude, it does in fact gradually reduce in size as the current moves from
its initial subtransient value towards the transient.
For reasons which it is not necessary to go into here, an
asymmetrical current is less difficult to break than a symmetrical one. Therefore, in order that the circuit-breaker
is able to deal with the most difficult case, it is required, when testing,
that the bolted fault shall continue long enough for the d.c. component to
decay to a specified level. This level
depends on the opening time of the breaker itself (i.e. from instant of trip
signal to separation of contacts) and may be of the order of 15%, after which
the current is regarded as 'symmetrical'.
At Switchgear Testing Stations a deliberate delay is introduced between
the onset of the fault and the trip signal to the breaker on test to ensure
that this is so.
In 3-phase switching the asymmetry will in general be partial in all
phases, as shown in Figure 4.2, and the percentages, taking account of sign,
will always add up to zero. (In Figure
4.2 they are -27 +97 -70 = 0.) If one phase happens to be symmetrical (0%
asymmetry) the other two, being displaced 120°, must both be partially asymmetrical.
The breaking capacities of circuit-breakers are always rated in kA
(or MVA) 'rms symmetrical'. The peak
asymmetrical current rating in kA may additionally be given. All system fault calculations are made to
determine the required rms symmetrical breaking current rating of the
switchgear to be installed.
This analysis is necessary if the amount of
fault current that will flow is to be correctly predicted but is beyond the
scope of this course.
However, if a
fault should develop somewhere in the system, that is to say a phase-to-phase
short-circuit or a phase-to-earth breakdown, then all connected generators will
at first feed extremely high currents into that fault, which will be limited
only by the impedance of the complete circuit from generator to fault. Fault currents can be ten or more times the
normal full-load current.
Such currents
will quickly cause intense overheating of conductors and windings, leading to
almost certain breakdown unless they are quickly disconnected. They will also give rise to severe mechanical
forces between the current-carrying conductors or windings. All such apparatus must be manufactured to
withstand these forces.
A fault current of 50000A
(rms) flowing in two busbars 3 inches apart will produce between them a peak
mechanical force of nearly half a ton-force per foot run of bars.
The purpose of
automatic protection is to remove the fault from the system and so break the
fault current as quickly as possible.
Before this can be achieved, however, the fault current will have flowed
for a finite, if small, time, and much heat energy will have been
released. Also the severe mechanical
forces referred to above will already have occurred and will have subjected all
conductors to intense mechanical stress.
FAULT CALCULATIONS
In order to predict the performance of a
protection scheme it is necessary to know what the fault conditions will
be. Although some relays will be
required to deal with overloads, undervoltages, etc., the majority will be
concerned with the detection of short-circuit conditions. To determine the fault level when a
short-circuit occurs requires a knowledge of the impedance of the various
components of the power system and the ability to calculate the current in
every part of the system.
IMPEDANCE
Although an impedance consists of a
resistance and a reactance it is usually sufficient to take only the reactance
into consideration in fault calculations.
If a computer is used for the calculation it is just as simple to
include resistance but if other means are used its inclusion is an unnecessary
complication. Inmost cases the exclusion
of resistance is justified in that the resistance is only a small fraction of
the impedance and even if it were as high as 20% it would only change the impedance
by about 2%.
The exception is in cables where, if the
cross-sectional area is small, the resistance is of the same order as the
reactance. However, as cables have a
very low impedance compared to transformers and generators the overall effect
of ignoring resistance is small.
FAULT LEVEL
When evaluating relay performance it is
usual to use the three phase fault level and, if earth-fault relays are
involved, the earth fault level. It is
appreciated that a phase-phase fault is far more likely than a three-phase
fault; however, the three-phase value is used on the basis that it is the most
onerous condition.
Calculation of a three-phase fault is
fairly straightforward as it is a balanced fault. That is, the current in each of the three
phases has the same magnitude and they are 120° apart. Therefore all that is
required is to calculate the current in one phase using the phase-neutral
voltage and the impedance per phase.
For example, an 11kV generator has an
impedance of 1.61W/phase:
|
phase voltage = = 6350V,
|
fault current = = 3944A,
Although current is used in determining
relay settings it is more usual to perform fault calculations in MVA as this
avoids complications when there is a change in voltage, i.e. when transformers are involved.
Therefore, fault level = 3 x 6350 x 3944 x
10-6 = 75MVA,
or Ö3 x 11kV x 3.94kA = 75MVA.
A quicker way would be to perform the
calculation in one operation,
|
viz. 3 x 11,000 x
x 10-6 = 75MVA
or in symbols
|
|||
|
|||
= x 10-6
or if V is in kV
|
fault MVA =
If the generator was rated as 15 MW, 0.8
power factor then the rating would be:
|
=
18.75 MVA.
The rating as a fraction of fault level
would be
|
=
¼ or 25%
This ratio is known as the percentage
impedance or Z%. Generator and
transformer impedances are generally expressed in this way
|
|||
|
|||
Z% = x 100% = x Z x 100%.
Another example Generator 12.5 MVA, 20%:
|
three-phase
fault level = x 100%
= 62.5 MVA.
Rather than calculate in percentages, and
multiply by 100% every time, it is convenient to use per unit values. For instance, 20% means every 20 in 100 and
it could be written 0.2 p.u., i.e. 0.2
in every 4.
Therefore, for the above generator Z
p.u. = 0.2:
|
three-phase
fault level = = 62.5
MVA.
or the
previous generator Z p.u. = 0.25:
|
three-phase
fault level = = 75
MVA.
It is also more convenient to convert all
per unit impedances to a common base, say 10 MVA, in the following manner:
|
18.75-MVA
generator Z p.u. = x 0.25 = 0.133 p.u..,
|
12.50-MVA
generator Z p.u. = x 0.2 = 0.16 p.u..
The reason for this is so that the relative
values of impedance can be attributed to every component in the circuit and
therefore allow easy calculations.
If a transformer rated at 4 MVA having an
impedance of 6% is connected to the 18.75 MVA generator and both impedances are
converted to a base of 10 MVA, then the generator impedance is 0.133 p.u. and
the transformer is
x =0.15
p.u. .
The fault level on the secondary side of
the transformer is
|
||||
|
||||
=
=35.3MVA.
If there were two 4 MVA transformers in
parallel each having an impedance of 6% then the total current impedance for a
fault on the secondary side would be
|
0.133 +
= 0.208 p.u.
and the fault level would be
|
= 48 MVA.
If one of the transformers instead of being
4MVA was 3MVA with an impedance of 6% then the system would be as Figure 4.3:
FIGURE 4.3 POWER
SYSTEM DIAGRAM
Zgen
= 0.133 p.u.
ZT1
= 0.15 p.u.
|
|||
|
|||
ZT2
= x =
0.2 p.u.
Z = 0.086 p.u..
and the fault level
|
By the application of Ohm's law the fault
current for any power system can be calculated by constructing an impedance
network in which all the components are represented by a per unit impedance and
the fault level is the "current" which is determined by dividing the
MVA base the "voltage"-by the
per unit impedance.
In the example the fault level is
45.7MVA. Across the two transformers in
parallel the "voltage" is 45.7 x 0.086 = 3.93 and therefore the
contribution to the fault through the 4MVA transformer is
|
= 26.2MVA
and through the 3MVA transformer
|
= 19.5MVA
Figure 4.3 shows the steps of calculation
starting with the system diagram with reactances at (a), the impedance diagram
at (b), the circuit reduction at (c) and (d) and the establishment of MVA flow
at (e) and (f) culminating in the system diagram with current flow at (g)
calculated from I = MVA/Ö3V. In an actual calculation some of these steps
would be omitted but the object remains the same. No matter how complicated the network is, the
object is to reduce it to a single impedance from which the fault MVA and its
flow in various parts of the circuit is determined so that the performance of
the protection can be predicted.
The elements of a power system are
specified as follows:
(a) Generators and Transformers-per cent
impedance on rating.
(b) Feeders and Interconnectors-actual impedance/phase.
(c) Reactors-voltage drop at rated current.
(b) Feeders and Interconnectors-actual impedance/phase.
(c) Reactors-voltage drop at rated current.
Typical impedance values can be attributed
to all components of a power system in the absence of definite
information. Transformer impedances are
usually easy to determine as the value is marked on the rating plate. The impedance of generators is usually of secondary
importance as most distribution systems generally have a much higher infeed and
fault contribution from the public electricity supply system. There is, however, a continuing increase in
offshore installations which there is no external supply. In this case the performance of the generator
is of prime importance.
GENERATORS
The performance of a generator under fault
conditions is more complicated than that of any other part of the distribution
system.
The fault current is initially about 8
times full-load current decaying rapidly to 5 times full-load current and then
decaying less rapidly to less than full-load current. The three stages are known as sub-transient,
transient and synchronous respectively.
The synchronous or steady-state reactance
of a generator is high because of armature reaction and is in the range of 4.5
to 2.5 p.u. at the machine rating. The
value used is made up of two components the actual reactance of the machine
which is small and a fictitious reactance.
When a fault occurs the current lags the voltage by 90° and the position of the field is such that it is demagnetised by
the current flowing in the stator conductors so that the air-gap flux and
therefore the generated e.m.f. is
low. Rather than use this low e.m.f. and
calculate the fault current by dividing it by the actual reactance it is more
convenient to use the initial e.m.f., E, and divide it by a fictitious value to
obtain the same result. The rapid change
of flux due to the demagnetising effect of the stator current results in an
induced current in the field which opposes the change and tends to maintain the
field flux. Thus the initial flux,
e.m.f. and fault current are somewhat higher than the steady-state value, and
decay exponentially towards the steady-state value. Once again a fictitious value of reactance
coupled with the e.m.f. is used in calculation-the reactance being termed the
transient value. There is one other
effect and that is the damper winding in the pole face will also produce a flux
opposing demagnetisation and will result in a fault current slightly higher
than that produced under transient conditions.
This fault current is of very short duration, it decays exponentially,
and the fictitious value associated with it is known as the subtransient
reactance.
The reactance values associated with a
generator are typically
·
Subtransient
reactance Xd" value 0.12 p.u.
·
Transient
reactance Xd' value 0.16 p.u.
·
Synchronous
reactance Xd value 2 p.u.
The e.m.f.
at no load would be the same as the system voltage, V, which at the nominal value is 4.
At any other load the e.m.f.
would be greater:
E" = [(V + X"d I sin f)2
+ (X"d I cos f)2]½,
E' = [(V + X'd I sin f)2
+ (X'd I cos f)2]½,
E = [(V + Xd I sin f)2
+ (Xd I cos f)2]½,
At normal system voltage where I is the
p.u. value of load = 1 at rated MVA and cosf is the power factor of the
load.
E" = [(1 + X"d I sin f)2
+ (X"d I cos f)2]½,
for the value given at full load 0.8 p.f.
E" = [(1 + 0.12 x 1 x 0.6) 2 = (0.12
x 1 x 0.8)2] ½,
E" = 4.076.
|
Subtransient current (or MVA) = = 8.97 X FL current
or 8.97 x rated MVA.
Another example:
at 70%
load, 0.9p.f.,
cosf=
0.9, f = 25.8°,
sinf=
0.436,
E' = [(1 +
0.16 x 0.7 x 0.436)2 + (0.16 x 0.7 X 0.9)2]½,
E' = 1.054.
|
Transient
current (or MVA) = = 6.58 x FL current
or 6.58 x
rated MVA.
The above are the initial values of the
current under short-circuit conditions.
The value would disappear in a fraction of second whilst it would take
several seconds for the transient value to decay.
The decay is exponential and typical time
constants are
T"d0
= 0.1s,
T'd0
= 5s.
These are open-circuit time constants,
under short-circuit conditions the value is modified as follows:
|
T"d
= T"d0.
|
T'd
= T'd0.
These would be the time constants for a
terminal fault. If the fault was on the
secondary side of a transformer, reactance XT, connected to the generator then
the short-circuit time constants would be
|
|
The subtransient current is of interest
only to the switchgear designer to determine closing duty. As far as protection is concerned it has
disappeared before any relay operation.
Both the transient and synchronous values
are used to determine the performance of the protection. The transient value for high-speed and
instantaneous schemes and the synchronous value for any scheme that has a time
delay.
In practice as soon as the fault occurs
there would be a reduction in voltage which would cause the automatic voltage
regulator to increase the field thus increasing the synchronous value from
no-load to the value for full load.
Figure 4.5 shows the values calculated above in a graphical form.
FIGURE
4.5 -
PERFORMANCE OF A 15MW GENERATOR UNDER FAULT CONDITIONS
CABLES
The resistance of a cable is determined by
the cross-sectional area of the conductors but the reactance depends on the
distance between the conductors, i.e.
the insulation thickness which depends on the voltage. The inductance can be calculated from
|
L = 0.46
log mH/m
where d is the distance between conductor
centres and r is the conductor geometric mean radius. It should be remembered that the cable made
from a number of strands and the radius which is calculated from area = pr2 is not the geometric mean radius which is
approximately 78% of that value. Also
the actual radius which is used in conjunction with the insulation thickness to
determine d is 15% larger than the calculated value.
Example 400 mm2 cable, 3-core screened,
6350/11000V
|
r = 0.78 x 11.28
= 8.8
insulation
thickness 5.6mm
d = (1.15 x
11.28)2 + 5.6 = 31.54 mm
|
L = 0.46 log =
0.255mH/m
and the reactance at 50Hz, X = 2pfL = 2p x 50 x 0.255 = 80 mW/m
Where three single-core cables are used
there is an increase in reactance because the distance between the conductors
is increased. A 400 mm2 single-core
cable has all overall diameter of 39 mm and therefore if the three cables
are mounted in trefoil formation (Fig
4.6(a)) then
|
L = 0.46 log =
0.297mH/m
and the reactance at 50Hz X = 93.4 mW/m
If the cables are laid flat as in Figure
4.6(b) then d is the geometric mean
distance which is:
d = (d1d2d3)1/3 = (39 x 39 x39 x 2)1/3 =
49.2 mm
|
L = 0.46 log =
0.343mH/m
and the reactance at 50Hz
X = 108 mW/m
There is no need to calculate the value in
every instance, a close approximation can be obtained by using typical values.
FIGURE
4.6 CABLE FORMATION
Reactance in mW/m
|
|
Three-core
|
Trefoil
|
Flat
|
|
11kV
|
80
|
95
|
110
|
|
415V
|
75
|
87
|
100
|
From the actual reactance the per unit
reactance at the chosen base can be calculated from
|
Z p.u. = x Z
(where V is in kV)
for example
1 km, 11kV three-core cable
X = 1000 x 80
x 10-6 = 0.08W
|
X p.u. =
x 0.08 = 0.0066pu
15m, 415 V,
three-core cable
X = 15 x 75 x
10-6 = 0.001125W
|
X p.u. =
x 0.001125 = 0.065pu
Comparison of the per unit reactance values
shows that the 415V cable will have a much greater effect on the fault current
than the much longer 11kV cable.
SOURCE IMPEDANCE
This is merely a value which represents the
impedance between the system under consideration and the source. The value is determined by the fault level at
the incoming busbar. If the actual fault
level is not known then a value based on the switchgear rupturing capacity is
used. For example, if the fault level or
rupturing capacity is 250 MVA then the source impedance on a 10 MVA base is
|
= 0.04pu
Figure 4.7(a) shows part of a typical
distribution system and Figure 4.7(b) the impedance diagram. As can be seen an impedance of 0.04 has been
included to limit the fault level at the plant substation 11kV busbars to 250
MVA.
MOTORS
There is also a contribution to a fault
from any induction motors which are connected at the time of the fault. The initial value will be roughly equal to
the motor-starting current but will decay rapidly to zero. It is mainly of interest to switchgear and
power system designers as the affect on differential protection is small and
the current will have disappeared by the time overcurrent relays operate. It could affect the operation of fast-acting
devices such as fuses or miniature circuit-breakers but the accuracy of these
devices is not of high order and therefore a precise appraisal is unnecessary.
Synchronous motors behave in the same way
as generators, the fault passing through the subtransient, transient to the
synchronous stage.
PRACTICAL EXAMPLES
Figure 4.7(a)
shows part of a typical distribution system.
There is an incoming 11 kV supply to the plant substation. Two 11kV interconnectors to the pump house
substation where there are two 11/0.415 kV transformers
The first step
is to construct an impedance diagram to a common base, say 10 MVA. The fault level at the plant substation 11 kV
busbars is 250 MVA and therefore the source impedance
|
Xs = = 0.04 p.u.
The two
interconnectors are each two 300 mm2 cables in parallel and therefore
the reactance of each interconnector is
½ x 600 x 80 x
10-6 = 0.024W
|
XI =
0.024 x = 0.002pu


FIGURE
4.7 SYSTEM, IMPEDANCE, MVA AND CURRENT
FLOW DIAGRAMS
The two 1.25
MVA transformers are each
|
|
||||
XT
= x = 0.48pu
The
interconnecting cables to the switchgear are assumed to be flat in
configuration:
½ x 25 x 100 x
10-6 = 0.00125W
|
XC =
0.00125 x = 0.0726pu
From this diagram the fault level at any
particular part can be determined. In
more complicated arrangements it may be necessary to calculate the combined
impedance of various parts of the system and redraw the impedance diagram to
simplify it to the extent where the calculation is straightforward. It may be that more than one redraw is
necessary before the calculation can be made.
Returning to the impedance diagram of the
system shown in Figure 4.7(b):
a fault at the
plant substation 11 kV busbar is
|
= 250 MVA, of course,
a fault at the
pump house substation 11kV busbar is
|
|
a fault at the
415V busbar is
|
|||
|
|||
with two
transformers, and
|
|||
|
|||
with one
transformer.
Note that if only one transformer is
connected the current per transformer is greater than if two transformers were
connected. The system diagram and the
flow through the various parts of the system is as shown in Figure 4.7(c).
Alternatively the actual current flow, marked in brackets, can be shown.
EARTH FAULTS
The earth-fault level of a distribution
system is determined by the method by which it is earthed. Although earthing at each substation is by
means of electrodes driven into the ground, very little of the earth-fault
current flows via this route.
In distribution system at the higher
voltages, i.e. 33kV, 11kV and 6.6kV, the
main earth-fault current flow is via the cable sheath and armouring whereas at
the utilisation voltages of 3.3kV and below the main earth fault is usually a
direct bonded conductor from the equipment to the distribution transformer.
Because the cable sheath and armouring are
used on the higher voltages the earth-fault path has a higher impedance than if
it was directly bonded. This means that
for an earth fault at a location removed from the substation where the
distribution transformer is installed a higher proportion of the voltage will
be dropped in the return path of a value such that the voltage at the fault
would be unacceptably high. It is for
this reason that all metalwork at each location must be earthed. When this is done it means that the whole
area is at high voltage and as such does not constitute a danger. It does, however, stress the insulation of
any connections between the fault area and the distribution point, e.g. pilot wires or telecommunications
circuits. Because of the latter there is
a requirement that the rise of earth voltage shall not exceed 430 V at any
point. To meet this requirement, in
general, requires that 33 kV, 11 kV and 6.6 kV systems be earthed via a neutral
earthing resistor.
The effect of a neutral earthing resistor
is to limit the earth-fault current to a relatively low value, which means that
during an earth fault most of the phase/neutral voltage is dropped across this
resistor.
The reduction in fault current is also
necessary so that the earth-fault current does not exceed the current-carrying
capability of the sheath and armour.
Table 4.1 gives typical resistance values for cable sheath and armour.
|
Conductor
size (mm2)
|
Lead
sheath
|
Steel
armour
|
Combined
|
|
50
|
1250
|
700
|
450
|
|
70
|
1050
|
650
|
400
|
|
95
|
950
|
600
|
370
|
|
120
|
870
|
570
|
340
|
|
150
|
760
|
540
|
310
|
|
185
|
700
|
500
|
290
|
|
240
|
570
|
460
|
250
|
|
300
|
500
|
340
|
200
|
|
400
|
430
|
310
|
180
|
TABLE
4.1. -
RESISTANCE OF LEAD SHEATH AND STEEL WIRE ARMOUR FOR THREE-CORE PILCSWA,
6350/11,000V CABLE
The value of resistance chosen for the
neutral earthing resistor is such that the earth-fault current is limited to
around the full-load current of the transformer and so, for the purpose of
assessing relay performance, it can be assumed that this will be the earth-fault
level of the whole system.
Usually each transformer will have its own neutral earthing resistor and all transformers in a group must be earthed. There will be, therefore, an earth-fault level throughout the system which, as far as the protection is concerned, is dependent only on the number of transformers connected.
Usually each transformer will have its own neutral earthing resistor and all transformers in a group must be earthed. There will be, therefore, an earth-fault level throughout the system which, as far as the protection is concerned, is dependent only on the number of transformers connected.
The earth-fault level of a 415 V system is
almost indeterminate. The rupturing
capacity of the switchgear is usually 31 MVA which is a maximum fault current
of 43,000 A and yet if the fault path has an impedance of only 0.1W the fault current is reduced to almost a twentieth of that value.
FIGURE 4.8
IMPEDANCE DIAGRAM SHOWING EARTH RETURN IMPEDANCE
As shown earlier cable impedance does have
a large effect on the fault level at 415V and a sufficiently accurate value of
earth-fault level can be obtained if the reactance of the return path is
assumed to be the same as the cable reactance from the transformer to the
fault. In other words, in the system
shown in Figure 4.8 for a fault at B the
three-phase fault level would be:
|
|||
|
|||
and the earth-fault level approximately
|
|||
|
|||
.jpg)




No comments:
Post a Comment